I had a special BLDC motor with 6 phases. To control the motor with a field-orientet control (FOC) I had to implement a 6-phase conversion from a 90° alpha/beta system into a 6-phase system. The performed equations look like this:
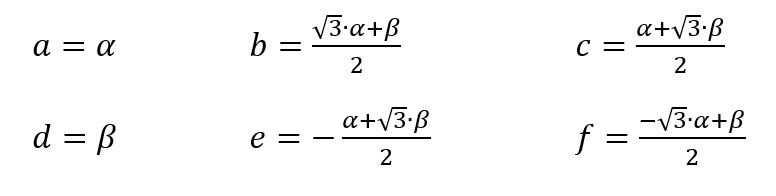
So, the alpha/beta signal is transformed into a 6-phase signal. This is a special case of the Inverse-Clarke-transformation that has quite narrow peaks of the six phases that is used in my special BLDC motor:
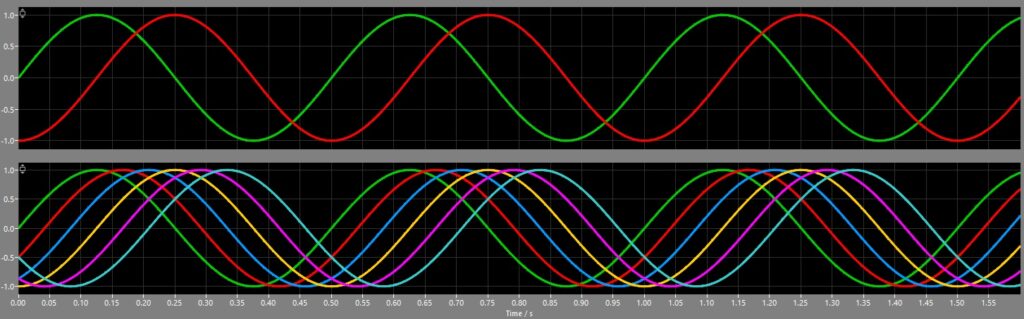
This is the logic for this:
VHDL
-- 6-phase Inverse Clarke transformation (alpha/beta -> abcdef)
-- Christian Noeding, christian@noeding-online.de
-- https://chrisdevblog.com | https://github.com/xn--nding-jua
--
-- Released under GNU General Public License v3
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
entity alpha_beta_to_abcdef is
generic (
output_scale : natural := 128
);
port(
clk : in std_logic;
alpha : in signed(31 downto 0); -- Q15.16
beta : in signed(31 downto 0); -- Q15.16
sync_in : in std_logic;
a : out signed(31 downto 0); -- Q15.16
b : out signed(31 downto 0); -- Q15.16
c : out signed(31 downto 0); -- Q15.16
d : out signed(31 downto 0); -- Q15.16
e : out signed(31 downto 0); -- Q15.16
f : out signed(31 downto 0); -- Q15.16
sync_out : out std_logic
);
end alpha_beta_to_abcdef;
architecture behavioural of alpha_beta_to_abcdef is
signal state : natural range 0 to 6 := 0;
signal alpha_scaled : signed(31 downto 0);
signal beta_scaled : signed(31 downto 0);
signal alpha_sqrt : signed(31 downto 0);
signal beta_sqrt : signed(31 downto 0);
--signals for multiplier
signal mult_in_a : signed(31 downto 0) := (others=>'0');
signal mult_in_b : signed(31 downto 0) := (others=>'0');
signal mult_out : signed(63 downto 0) := (others=>'0');
begin
-- multiplier
process(mult_in_a, mult_in_b)
begin
mult_out <= mult_in_a * mult_in_b;
end process;
process(clk)
begin
if rising_edge(clk) then
if (sync_in = '1' and state = 0) then
mult_in_a <= alpha;
mult_in_b <= to_signed(output_scale * 2**16, 32);
state <= 1; -- start state-machine
elsif (state = 1) then
alpha_scaled <= resize(shift_right(mult_out, 16), 32);
mult_in_a <= beta;
mult_in_b <= to_signed(output_scale * 2**16, 32);
state <= state + 1;
elsif (state = 2) then
beta_scaled <= resize(shift_right(mult_out, 16), 32);
mult_in_a <= to_signed(56755, 32); -- sqrt(3)/2 as Q15.16
mult_in_b <= alpha_scaled;
state <= state + 1;
elsif (state = 3) then
alpha_sqrt <= resize(shift_right(mult_out, 16), 32); -- sqrt(3)*0.5*alpha in Q15.16
mult_in_a <= to_signed(56755, 32); -- sqrt(3)/2 as Q15.16
mult_in_b <= beta_scaled;
state <= state + 1;
elsif (state = 4) then
beta_sqrt <= resize(shift_right(mult_out, 16), 32); -- sqrt(3)*0.5*beta in Q15.16
state <= state + 1;
elsif (state = 5) then
-- calculation for 6-phase with 60° phase-shift
--a <= alpha_scaled;
--b <= shift_right(alpha_scaled, 1) + beta_sqrt; -- 0.5*alpha + 0.866025404*beta
--c <= -shift_right(alpha_scaled, 1) + beta_sqrt; -- -0.5*alpha + 0.866025404*beta
--d <= -alpha_scaled;
--e <= -shift_right(alpha_scaled, 1) - beta_sqrt; -- -0.5*alpha - 0.866025404*beta
--f <= shift_right(alpha_scaled, 1) - beta_sqrt; -- 0.5*alpha - 0.866025404*beta
-- calculation for 6-phase with 30° phase-shift
a <= alpha_scaled;
b <= alpha_sqrt + shift_right(beta_scaled, 1);
c <= shift_right(alpha_scaled, 1) + beta_sqrt;
d <= beta_scaled;
e <= -shift_right(alpha_scaled, 1) + beta_sqrt;
f <= -alpha_sqrt + shift_right(beta_scaled, 1);
sync_out <= '1';
state <= state + 1;
elsif (state = 6) then
sync_out <= '0';
state <= 0;
end if;
end if;
end process;
end behavioural;
